Золотое сечение и числа последовательности Фибоначчи. June 14th, 2011
Некоторое время назад я обещала прокомментировать утверждение Толкачева о том, что Питер построен по принципу Золотого Сечения, а Москва – по принципу симметрии, и что именно поэтому столь ощутимы различия в восприятии этих двух городов, и именно поэтому петербуржец, приезжая в Москву «заболевает головой», а москвич «заболевает головой», приезжая в Питер. Требуется некоторое время для сонастройки с городом (как при перелете в штаты – требуется сонастройка со временем).
Дело в том, что наш глаз смотрит - ощупывая пространство с помощью определенных движений глаз – саккад (в переводе – хлопок паруса). Глаз совершает «хлопок» и посылает сигнал в мозг «сцепление с поверхностью произошло. Все в порядке. Информация такая-то». И в течение жизни глаз привыкает к определенной ритмике этих саккад. И когда эта ритмика кардинально меняется (с городского пейзажа на лес, с Золотого Сечения на симметрию) – тут то и требуется некоторая работа мозга по перенастройке.
Теперь подробности:
Определение ЗС - это деление отрезка на две части в таком соотношении, при котором большая часть относится к меньшей, как их сумма (весь отрезок) к большей.
То есть, если мы примем весь отрезок c за 1, то отрезок a будет равен 0,618, отрезок b - 0,382. Таким образом, если взять строение, например, храм, построенный по принципу ЗС, то при его высоте скажем 10 метров, высота барабана с куполом будут равны 3,82 см, а высота основания строения будет 6, 18 см. (понятно, что цифры я взяла ровными для наглядности)

А какова связь между ЗС и числами Фибоначчи?
Числа последовательности Фибоначчи это:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597…
Закономерность чисел в том, что каждое последующее число равно сумме двух предыдущих чисел.
0 + 1 = 1;
1 + 1 = 2;
2 + 3 = 5;
3 + 5 = 8;
5 + 8 = 13;
8 + 13 = 21 и т.д.,
а отношение смежных чисел приближается к отношению ЗС.
Так, 21: 34 = 0,617, а 34: 55 = 0,618.
То есть в основе ЗС лежат числа последовательности Фибоначчи.
Вот этот ролик ещё раз наглядно демонстрирует эту связь ЗС и чисел Фибоначчи
Где ещё встречаются принцип ЗС и числа последовательности Фибоначчи?
Листья у растений описывается последовательностью Фибоначчи. Зерна подсолнуха, сосновые шишки, лепестки цветков, ячейки ананаса также располагаются согласно последовательности Фибоначчи.
Яйцо птицы
Длины фаланг пальцев человека относятся примерно как числа Фибоначчи. Золотое сечение просматривается в пропорциях лица.
Эмиль Розенов исследовал ЗС в музыке эпохи Барокко и классицизма на примере произведений Баха, Моцарта, Бетховена.
Известно, что Сергей Эйзенштейн искусственно построил фильм «Броненосец Потёмкин» по правилам ЗС. Он разбил ленту на пять частей. В первых трёх действие развивается на корабле. В двух последних - в Одессе, где разворачивается восстание. Этот переход в город происходит точно в точке золотого сечения. Да и в каждой части есть свой перелом, происходящий по закону золотого сечения. В кадре, сцене, эпизоде происходит некий скачок в развитии темы: сюжета, настроения. Эйзенштейн считал, что, так как такой переход близок к точке золотого сечения, он воспринимается как наиболее закономерный и естественный.
Многие элементы декора, а так же шрифты, созданы с использованием ЗС. Например шрифт А.Дюрера (в рисунке буква «А»)
Считается, что термин «Золотое сечение» ввел Леонардо Да Винчи, который говорил, «пусть никто, не будучи математиком, не дерзнет читать мои труды” и показывал пропорции человеческого тела на своём знаменитом рисунке «Витрувианский человек». “Если мы человеческую фигуру – самое совершенное творение Вселенной – перевяжем поясом и отмерим потом расстояние от пояса до ступней, то эта величина будет относиться к расстоянию от того же пояса до макушки, как весь рост человека к длине от пояса до ступней”.
Знаменитый портрет Моны Лизы или Джоконды (1503) создан по принципу золотых треугольников.
Собственно говоря сама звезда или пентакль представляет собой построение ЗС.
Ряд чисел Фибоначчи наглядно моделируется (материализуется) в форме спирали
А в природе спираль ЗС выглядит вот так:
При этом, спираль наблюдается повсеместно
(в природе и не только):
- Семена в большинстве растений расположены по спирали
- Паук плетет паутину по спирали
- Спиралью закручивается ураган
- Испуганное стадо северных оленей разбегается по спирали.
- Молекула ДНK закручена двойной спиралью. Молекулу ДНК составляют две вертикально переплетенные спирали длиной 34 ангстрема и шириной 21 ангстрема. Числа 21 и 34 следуют друг за другом в последовательности Фибоначчи.
- Эмбрион развивается в форме спирали
- Спираль «улитки во внутреннем ухе»
- Вода уходит в слив по спирали
- Спиральная динамика показывает развитие личности человека и его ценностей по спирали.
- Ну и конечно, сама Галактика имеет форму спирали
Таким образом можно утверждать, что сама природа построена по принципу Золотого Сечения, оттого эта пропорция гармоничнее воспринимается человеческим глазом. Она не требует «исправления» или дополнения получаемой картинки мира.
Теперь о Золотом сечении в архитектуре
Пирамида Хеопса представляет собой пропорции ЗС. (Фотография нравится – с заваленным песком Сфинксом).
Согласно Ле Корбюзье, в рельефе из храма фараона Сети I в Абидосе и в рельефе, изображающем фараона Рамзеса, пропорции фигур соответствуют золотому сечению. В фасаде древнегреческого храма Парфенона также присутствуют золотые пропорции.
Собор "Нотредам де Пари" в Париже, Франция.
Одно из выдающихся строений, выполненных по принципу ЗС – Смольный Собор в Питере. К собору ведут по краям две дорожки и если приближаться по ним к собору, то тот будто приподнимается в воздухе.
В Москве также есть строения выполненные с использованием ЗС. Например, Храм Василия Блаженного
Однако застройка, использующая принципы симметрии преобладает.
Например, Кремль и Спасская башня.
Высота стен Кремля также нигде не отражает принципа ЗС относительно высоты башен, например. Или взять гостиницу Россия, или гостиницу Космос.
При этом здания, построенные по принципу ЗС представляют больший процент в Питере, при этом это здания уличной застройки. Литейный проспект.
Таким образом, Золотое Сечение использует коэффицент 1,68, а симметрия 50/50.
То есть симметричные здания построены по принципу равенства сторон.
Ещё одной важной характеристикой ЗС является её динамичность и стремление к разворачиванию, за счет последовательности чисел Фибоначчи. Тогда как симметрия – наоборот представляет собой стабильность, устойчивость и неподвижность.
Кроме этого, дополнительное ЗС вносит в план Питера обилие водных пространств, расплескавшихся по городу и диктующих подчиненность города их изгибам. Да и сама схема Питера напоминает спираль или зародыш одновременно.
Папа, правда, высказал другую версию, отчего у москвичей и питерцев «голова болит» при посещении столиц. Папа относит это к энергиям городов:
Санкт-Петербург – имеет мужской род и соответственно мужские энергии,
Ну а Москва – соответственно – женского рода и обладает женскими энергиями.
Так жителям столиц, настроившимся на свой определенный баланс женского и мужского в своих организмах – сложно перестраиваться при посещении города-соседа, а у кого-то может и сложности какие-то имеются с восприятием одной или другой энергий и оттого город сосед могут и вовсе не любить!
В подтверждение этой версии говорит и то, что все российские императрицы правили именно в Питере, тогда как Москва видела лишь царей мужского пола!
Использованные ресурсы.
Человек различает окружающие его предметы по форме. Интерес к форме какого-либо предмета может быть продиктован жизненной необходимостью, а может быть вызван красотой формы. Форма, в основе построения которой лежат сочетание симметрии и золотого сечения, способствует наилучшему зрительному восприятию и появлению ощущения красоты и гармонии. Целое всегда состоит из частей, части разной величины находятся в определённом отношении друг к другу и к целому. Принцип золотого сечения – высшее проявление структурного и функционального совершенства целого и его частей в искусстве, науке, технике и природе.
Золотое сечение – гармоническая пропорция
В математике пропорцией (лат. proportio) называют равенство двух отношений:
a : b = c : d .
Отрезок прямой AB можно разделить на две части следующими способами:
- на две равные части – AB : AC = AB : BC ;
- на две неравные части в любом отношении (такие части пропорции не образуют);
- таким образом, когда AB : AC = AC : BC .
Последнее и есть золотое деление или деление отрезка в крайнем и среднем отношении.
Золотое сечение – это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей; или другими словами, меньший отрезок так относится к большему, как больший ко всему:
a
: b
= b
: c
или
c
: b
= b
: a
.
Рис. 1. Геометрическое изображение золотой пропорции
Практическое знакомство с золотым сечением начинают с деления отрезка прямой в золотой пропорции с помощью циркуля и линейки.
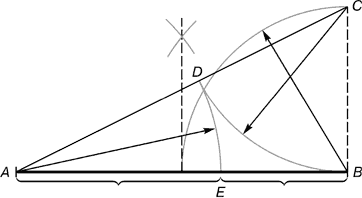
Рис. 2. BC = 1/2 AB ; CD = BC
Из точки B восставляется перпендикуляр, равный половине AB . Полученная точка C соединяется линией с точкой A . На полученной линии откладывается отрезок BC , заканчивающийся точкой D . Отрезок AD переносится на прямую AB . Полученная при этом точка E делит отрезок AB в соотношении золотой пропорции.
Отрезки золотой пропорции выражаются бесконечной иррациональной дробью AE = 0,618..., если AB принять за единицу, BE = 0,382... Для практических целей часто используют приближённые значения 0,62 и 0,38. Если отрезок AB принять за 100 частей, то большая часть отрезка равна 62, а меньшая – 38 частям.
Свойства золотого сечения описываются уравнением:
x 2 – x – 1 = 0.
Решение этого уравнения:

Свойства золотого сечения создали вокруг этого числа романтический ореол таинственности и чуть ли не мистического поклонения.
Второе золотое сечение
Болгарский журнал «Отечество» (№10, 1983 г.) опубликовал статью Цветана Цекова-Карандаша «О втором золотом сечении», которое вытекает из основного сечения и даёт другое отношение 44: 56.
Такая пропорция обнаружена в архитектуре, а также имеет место при построении композиций изображений удлинённого горизонтального формата.

Рис. 3.
Деление осуществляется следующим образом. Отрезок AB делится в пропорции золотого сечения. Из точки C восставляется перпендикуляр CD . Радиусом AB находится точка D , которая соединяется линией с точкой A . Прямой угол ACD делится пополам. Из точки C проводится линия до пересечения с линией AD . Точка E делит отрезок AD в отношении 56: 44.

Рис. 4.
На рисунке показано положение линии второго золотого сечения. Она находится посередине между линией золотого сечения и средней линией прямоугольника.
Золотой треугольник
Для нахождения отрезков золотой пропорции восходящего и нисходящего рядов можно пользоваться пентаграммой .

Рис. 5. Построение правильного пятиугольника и пентаграммы
Для построения пентаграммы необходимо построить правильный пятиугольник. Способ его построения разработал немецкий живописец и график Альбрехт Дюрер (1471...1528). Пусть O – центр окружности, A – точка на окружности и E – середина отрезка OA . Перпендикуляр к радиусу OA , восставленный в точке O , пересекается с окружностью в точке D . Пользуясь циркулем, отложим на диаметре отрезок CE = ED . Длина стороны вписанного в окружность правильного пятиугольника равна DC . Откладываем на окружности отрезки DC и получим пять точек для начертания правильного пятиугольника. Соединяем углы пятиугольника через один диагоналями и получаем пентаграмму. Все диагонали пятиугольника делят друг друга на отрезки, связанные между собой золотой пропорцией.
Каждый конец пятиугольной звезды представляет собой золотой треугольник. Его стороны образуют угол 36° при вершине, а основание, отложенное на боковую сторону, делит её в пропорции золотого сечения.

Рис. 6. Построение золотого треугольника
Проводим прямую AB . От точки A откладываем на ней три раза отрезок O произвольной величины, через полученную точку P проводим перпендикуляр к линии AB , на перпендикуляре вправо и влево от точки P откладываем отрезки O . Полученные точки d и d 1 соединяем прямыми с точкой A . Отрезок dd 1 откладываем на линию Ad 1 , получая точку C . Она разделила линию Ad 1 в пропорции золотого сечения. Линиями Ad 1 и dd 1 пользуются для построения «золотого» прямоугольника.
История золотого сечения
Принято считать, что понятие о золотом делении ввёл в научный обиход Пифагор , древнегреческий философ и математик (VI в. до н.э.). Есть предположение, что Пифагор своё знание золотого деления позаимствовал у египтян и вавилонян. И действительно, пропорции пирамиды Хеопса , храмов, барельефов, предметов быта и украшений из гробницы свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создании. Французский архитектор Ле Корбюзье нашёл, что в рельефе из храма фараона Сети I в Абидосе и в рельефе, изображающем фараона Рамзеса, пропорции фигур соответствуют величинам золотого деления. Зодчий Хесира, изображённый на рельефе деревянной доски из гробницы его имени, держит в руках измерительные инструменты, в которых зафиксированы пропорции золотого деления.
Греки были искусными геометрами. Даже арифметике обучали своих детей при помощи геометрических фигур. Квадрат Пифагора и диагональ этого квадрата были основанием для построения динамических прямоугольников.

Рис. 7. Динамические прямоугольники
Платон (427...347 гг. до н.э.) также знал о золотом делении. Его диалог «Тимей» посвящён математическим и эстетическим воззрениям школы Пифагора и, в частности, вопросам золотого деления.
В фасаде древнегреческого храма Парфенона присутствуют золотые пропорции. При его раскопках обнаружены циркули, которыми пользовались архитекторы и скульпторы античного мира. В Помпейском циркуле (музей в Неаполе) также заложены пропорции золотого деления.

Рис. 8.
В дошедшей до нас античной литературе золотое деление впервые упоминается в «Началах» Евклида . Во 2-й книге «Начал» даётся геометрическое построение золотого деления. После Евклида исследованием золотого деления занимались Гипсикл (II в. до н.э.), Папп (III в. н.э.) и др. В средневековой Европе с золотым делением познакомились по арабским переводам «Начал» Евклида. Переводчик Дж. Кампано из Наварры (III в.) сделал к переводу комментарии. Секреты золотого деления ревностно оберегались, хранились в строгой тайне. Они были известны только посвящённым.
В эпоху Возрождения усиливается интерес к золотому делению среди учёных и художников в связи с его применением как в геометрии, так и в искусстве, особенно в архитектуре Леонардо да Винчи , художник и учёный, видел, что у итальянских художников эмпирический опыт большой, а знаний мало. Он задумал и начал писать книгу по геометрии, но в это время появилась книга монаха Луки Пачоли, и Леонардо оставил свою затею. По мнению современников и историков науки, Лука Пачоли был настоящим светилом, величайшим математиком Италии в период между Фибоначчи и Галилеем. Лука Пачоли был учеником художника Пьеро делла Франчески , написавшего две книги, одна из которых называлась «О перспективе в живописи». Его считают творцом начертательной геометрии.
Лука Пачоли прекрасно понимал значение науки для искусства. В 1496 г. по приглашению герцога Моро он приезжает в Милан, где читает лекции по математике. В Милане при дворе Моро в то время работал и Леонардо да Винчи. В 1509 г. в Венеции была издана книга Луки Пачоли «Божественная пропорция» с блестяще выполненными иллюстрациями, ввиду чего полагают, что их сделал Леонардо да Винчи. Книга была восторженным гимном золотой пропорции. Среди многих достоинств золотой пропорции монах Лука Пачоли не преминул назвать и её «божественную суть» как выражение Божественного Триединства – Бог Отец , Бог Сын и Бог Дух Святой (подразумевалось, что малый отрезок есть олицетворение Бога Сына, больший отрезок – Бога Отца, а весь отрезок – Бога Духа Святого).
Электронные книги:
- Марио Ливио.
ГОУ Гимназия №1505
«Московская городская педагогическая гимназия-лаборатория»
Реферат
Числа Фибоначчи и Золотое сечение
Азов Никита
Руководитель: Шалимова М.Н.
Введение ………………………………………………….……………2
Глава 1
История Чисел Фибоначчи.………………………………..……..5
Глава 2
Числа Фибоначчи как возвратная прогрессия………...…...……………………………………..….....12
Глава 3
Числа Фибоначчи и Золотое сечение………………………
Заключение …………………………………………………...…...16
Список литературы ………………………………………………………………….……..20
Введение.
Актуальность исследования. На мой взгляд в настоящие дни уделяется мало внимания математическим теоремам и фактам, известным из истории развития науки. На примере чисел Фибоначчи я хотел бы показать насколько они могут глобальны и широко применимы не только в математике, но и в повседневной жизни.
Целью моей работы является изучение истории, свойств, применения и связей чисел Фибоначчи с золотым сечением.
Глава 1. Числа Фибоначчи и их история.
Леонардо (1170-1250гг.) был рожден в Пизе. В последствии получил прозвище Фибоначчи, что означает «хорошо рожденный сын». Его отец торговал в арабских странах Северной Африки. Там Леонардо изучал математику с арабскими учителями, а также знакомился с достижениями индийских и древнегреческих ученых по трактатам в арабском переводе. Усвоив весь изучаемый им материал, он создал собственную книгу – «Книгу абака» (первое издание было написано в 1202 году, но до нас сохранилось только переиздание 1228 года). Таким образом, он стал первым средневековым выдающимся математиком, а также ознакомил Европу с арабскими цифрами и десятичной системой вычисления, которой мы пользуемся каждый день с ранних лет и до самой старости.«Книгу абака» можно разделить на пять частей по содержанию. Первые пять глав книги посвящены арифметике целых числе на основе десятичной нумерации. В 6-7 главе описаны действия над обыкновенными дробями. В 8-10 главе описаны приемы решения задач с помощью пропорций. В 11 главе рассматриваются задачи на смешение, в 12 главе речь идет о так называемых числах Фибоначчи. Далее описаны еще некоторые приемы с числами и приведены задачи на разные темы.
Основная задача поясняющая возникновение ряда чисел Фибоначчи – задача о кроликах. Вопрос задачи звучит так: «Сколько пар кроликов в один год рождается от одной пары?». К задаче дано пояснение, что пара кроликов через месяц рождает еще одну пару, а по природе кролики начинают рожать потомство на второй месяц после своего рождения. Автор дает нам решение задачи. Получается, что в первый месяц первая пара родит еще одну. Во второй первая пара родит еще одну – будет три пары. В 3-ий месяц родят две пары – изначально данная и рожденная в первый месяц. Получается 5 пар. И так далее, используя такую же логику в рассуждении мы получим, что в четвертый месяц будет 8 пар, в пятый 13, в шестой 21, в седьмлй 34, в в восьмой 55, в девятый 89, в дестый 144, в одиннадцатый 233, в двенадцатый 377.

Мы можем обозначить кол-во кроликов в любой из двенадцати месяцев как u n. Мы получаем ряд чисел:
В ряде этих чисел каждый член равен сумме двух предыдущих. Получается, что любой член уравнения можно определить по уравнению:
Рассмотрим важный частный случай для этого уравнения, когда u 1 и u 2 =1. Мы получим последовательность чисел 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377… Эту же последовательность чисел мы получали в задачу про кроликов. Эти числа названы числами Фибоначчи в честь автора.
Эти числа а также уравнение (2) обладает многими свойствами, который будут рассматриваться в моей работе.
Глава 2. Связь между рядом Чисел Фибоначчи и прогрессиями. Основные свойства ряда.
Для того, чтобы вывести основные свойства ряда возьмем как пример первые пять чисел: 1, 1, 2, 3, 5, 8. Мы видим, что каждое новое число равно сумме двух предыдущих. Отсюда мы можем вывести формулу получения любого числа ряда, а также формулу суммы любого кол-ва чисел из ряда.
Мы видим, что формулы кардинально отличаются от формул свойственных арифметической и геометрической прогрессий. А также мы можем сказать что только первые два числа из ряда могут относится к каким либо прогрессиям.
У арифметической и геометрических прогрессий имеются только две ранее упомянутые формулы, и чтобы посчитать например сумму четных, нечетных или сумму квадратов чисел каждый раз приходится решать задачу для отдельно взятого ряда. Но так как ряд чисел Фибоначчи является неизменным (не имеет шагов, знаменателей и различных первых членов прогрессии), то это значит, что для него можно вывести формулу получения сумм отдельных элементов ряда. Вот например формула для получения суммы чисел ряда под четными номерами:
Существует аналогичная формула для чисел из ряда под нечетными номерами:
Также есть формула для получения суммы чисел из ряда возведенных в квадрат:
У чисел Фибоначчи есть еще одно уникальное свойство, которое нехарактерно для для арифметической и геометрической прогрессий. Отношение ряда чисел (предыдущего к последующему) постоянно стремится к значению 0.618, аналогичная ситуация происходит при делении F n на F n +2 (отношение стремится к 0.382), при делении F n на F n +3 (отношение стремится к 0.236) и так далее. В итоге мы получили набор отношений. Набор их значений и значений обратных им называются фибоначчиевы коэффициенты. А значение обратное 0.618 – 1.618, является числом
(«фи»). Он также является одним из пары корней характерического для ряда многочлена x 2 -x-1.Глава 3. Золотое сечение и числа Фибоначчи.
Золотое сечение (золотая пропорция, деление в крайнем и среднем отношении) - деление непрерывной величины на две части в таком отношении, при котором меньшая часть так относится к большей, как большая ко всей величине.
Попробуем объяснить это на примере бесконечной прямой. Примем всю прямую с за единицу. Разделим ее на две части a и b, которые делят прямую на отрезки равный по отношению к 1, как 0.618 и 0.382 соответственно. А эти числа являются одними из коэффициентов ряда чисел Фибоначчи. Мы получаем, что отношение больших частей этой прямой к меньшим асимптотически приближается к числу
.
Существует две основные фигуры, в которых отражается принцип золотого сечения.
Золотое сечение было известно еще древним грекам. Архимед считается открывателем Архимедовой спирали. Её смысл состоит в том, что каждый новый завиток увеличивается в определенное число, и отношение этих завитков равно числу
.
Вторая фигура – золотой треугольник. Это равнобедренный треугольник, в котором отношение боковых сторон к основанию равно
Окружающий мир, начиная с мельчайших невидимых частиц, и заканчивая далекими галактиками бескрайнего космоса, таит в себе много неразгаданных тайн. Однако над некоторыми из них уже приподнята завеса таинственности благодаря пытливым умам ряда ученых.
Одним из таких примеров является «золотое сечение» и числа Фибоначчи , составляющие его основу. Данная закономерность получила отображение в математическом виде и часто встречается в окружающей человека природе, еще раз исключая вероятность того, что она возникла в результате случая.
Числа Фибоначчи и их последовательность
Последовательностью чисел Фибоначчи называется ряд чисел, каждое из которых является суммой двух предыдущих:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377 …
Особенностью этой последовательности являются числовые значения, которые получаются вследствие деления чисел этого ряда друг на друга.
Ряд чисел Фибоначчи имеет свои интересные закономерности:
- В ряду чисел Фибоначчи, каждое число разделенное на следующее будет показывать значение, стремящееся к 0,618 . Чем дальше числа от начала ряда, тем точнее будет соотношение. К примеру, цифры взятые в начале ряда 5 и 8 будут показывать 0,625 (5/8=0,625 ). Если же взять числа 144 и 233 , то они покажут соотношение 0.618 .
- В свою очередь, если в ряду чисел Фибоначчи разделить число на предыдущее, то результат деления будет стремится к 1,618 . Для примера использованы те же цифры, что оговаривались выше: 8/5=1,6 и 233/144=1,618 .
- Число поделенное на следующее за ним через одно, будет показывать значение, приближающееся к 0,382 . И чем дальше от начала ряда взяты цифры, тем точнее значение соотношения: 5/13=0,385 и 144/377=0,382 . Деление цифр в обратном порядке будет давать результат 2,618 : 13/5=2,6 и 377/144=2,618 .
Используя вышеописанные методы расчета и увеличивая промежутки между цифрами можно вывести следующий ряд значений: 4.235, 2.618, 1.618, 0.618, 0.382, 0.236, который широко применяется в инструментах Фибоначчи на рынке форекс.
Золотое сечение или Божественная пропорция
Очень наглядно представляет «золотое сечение» и числа Фибоначчи аналогия с отрезком. Если отрезок АВ разделить точкой С в таком соотношении, чтобы соблюдалось условие:
АС/ВС=ВС/АВ, тогда это будет «золотое сечение»
ЧИТАЙТЕ ТАКЖЕ СЛЕДУЮЩИЕ СТАТЬИ:
Удивительно, но именно это соотношение прослеживается в ряду чисел Фибоначчи. Взяв несколько цифр из ряда, можно расчетом проверить, что это так. Например, такая последовательность чисел Фибоначчи …55, 89, 144 … Пусть число 144 является целым отрезком АВ, о котором упоминалось выше. Поскольку 144 является суммой двух предыдущих чисел, то 55+89=АС+ВС=144.
Деление отрезков покажет следующие результаты:
АС/ВС=55/89=0,618
ВС/АВ=89/144=0,618
Если принять отрезок АВ за целое, или за единицу, то АС=55 будет составлять 0,382 от этого целого, а ВС=89 будет равным 0,618.
Где встречаются числа Фибоначчи
Закономерную последовательность чисел Фибоначчи знали греки и египтяне еще задолго до самого Леонардо Фибоначчи. Такое название этот числовой ряд приобрел после того, как знаменитый математик обеспечил широкое распространение этого математического феномена в ученых рядах.
Важно отметить, что золотые числа Фибоначчи являются не просто наукой, а математическим отображением окружающего мира. Множество природных явлений, представителей растительного и животного мира имеет в своих пропорциях «золотое сечение». Это и спиралевидные завитки раковины, и расположение семян подсолнуха, кактусы, ананасы.
Спираль, пропорции ответвлений которой подчинены закономерностям «золотого сечения», лежит в основе образования урагана, плетения паутины пауком, формы многих галактик, переплетения молекул ДНК и множества других явлений.
Длина хвоста ящерицы к ее туловищу имеет соотношение 62 к 38. Отросток цикория, перед тем как выпустить листок, делает выброс. После того, как первый лист выпущен, происходит второй выброс перед выпуском второго листа, по силе равный 0,62 от условно принятой единицы силы первого выброса. Третий выброс равен 0,38, а четвертый - 0,24.
Для трейдера также большое значение имеет тот факт, что движение цены на рынке форекс часто подчинено закономерности золотых чисел Фибоначчи. На основе этой последовательность создан целый ряд инструментов, которые трейдер может использовать в своем арсенале
Часто используемый трейдерами инструмент « » может с высокой точностью показывать цели движения цены, а также уровни ее коррекции.
Последовательность Фибоначчи в математике и в природе
Последовательность Фибоначчи , известная всем по фильму "Код Да Винчи" - ряд цифр, описанный в виде загадки Итальянским математиком Леонардо Пизанским, более известным под прозвищем Фибоначчи, в XIII веке. Вкратце суть загадки:
Кто-то поместил пару кроликов в некоем замкнутом пространстве, чтобы узнать, сколько пар кроликов родится при этом в течении года, если природа кроликов такова, что каждый месяц пара кроликов производит на свет другую пару, а способность к производству потомства у них появляется по достижению двухмесячного возраста.

В итоге получается такая последовательность: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 , где через запятую показано количество пар кроликов в каждом из двенадцати месяцев.
Эту последовательность можно продолжать бесконечно долго. Её суть в том, что каждое следующее число является суммой двух предыдущих.
У этой последовательности есть ряд математических особенностей, которых обязательно нужно коснуться. Данная последовательность асимптотически (приближаясь все медленнее и медленнее) стремится к некоторому постоянному соотношению. Однако, это соотношение иррационально, то есть представляет собой число с бесконечной, непредсказуемой последовательностью десятичных цифр в дробной части. Его невозможно выразить точно.
Так отношение какого-либо члена последовательности к предшествующему ему колеблется около числа 1,618 , через pаз то превосходя, то не достигая его. Отношение к следующему аналогично приближается к числу 0,618 , что обратно пропорционально 1,618 . Если мы будем делить элементы последовательности через одно, то получим числа 2,618 и 0,382 , которые так же являются обратно пропорциональными. Это так называемые коэффициенты Фибоначчи.
К чему всё это? Так мы приближаемся к одному из самых загадочных явлений природы. Фибоначчи по сути не открыл ничего нового, он просто напомнил миру о таком явлении, как Золотое Сечение , которое не уступает по значимости теореме Пифагора
Все окружающие нас предметы мы различаем в том числе и по форме. Какие-то нам нравятся больше, какие-то меньше, некоторые вовсе отталкивают взгляд. Иногда интерес может быть продиктован жизненной ситуацией, а порой красотой наблюдаемого объекта. Симметричная и пропорциональная форма, способствует наилучшему зрительному восприятию и вызывает ощущение красоты и гармонии. Целостный образ всегда состоит из частей разного размера, находящихся в определённом соотношении друг с другом и целым.
Золотое сечение - высшее проявление совершенства целого и его частей в науке, искусстве и природе.
Если на простом примере, то Золотое Сечение - это деление отрезка на две части в таком соотношении, при котором большая часть относится к меньшей, как их сумма (весь отрезок) к большей.

Если мы примем весь отрезок c за 1 , то отрезок a будет равен 0,618 , отрезок b - 0,382 , только так будет соблюдено условие Золотого Сечения (0,618/0,382=1,618 ; 1/0,618=1,618 ). Отношение c к a равно 1,618 , а с к b2,618 . Это всё те же, уже знакомые нам, коэффициенты Фибоначчи.
Разумеется есть золотой прямоугольник, золотой треугольник и даже золотой кубоид. Пропорции человеческого тела во многих соотношениях близки к Золотому Сечению.

Изображение: marcus-frings.de

Но самое интересное начинается, когда мы объединим полученные знания. На рисунке наглядно показана связь между последовательностью Фибоначчи и Золотым сечением. Мы начинаем с двух квадратов первого размера. Сверху добавляем квадрат второго размера. Подрисовываем рядом квадрат со стороной, равной сумме сторон двух предыдущих, третьего размера. По аналогии появляется квадрат пятого размера. И так далее пока не надоест, главное, чтобы длина стороны каждого следующего квадрата равнялась сумме длин сторон двух предыдущих. Мы видим серию прямоугольников, длины сторон, которых являются числами Фибоначчи, и, как не странно, они называются прямоугольниками Фибоначчи.
Если мы проведём плавную линий через углы наших квадратов, то получим ни что иное, как спираль Архимеда, увеличение шага которой всегда равномерно.

Ничего не напоминает?

Фото: ethanhein on Flickr
И не только в раковине моллюска можно найти спирали Архимеда, а во многих цветах и растениях, просто они не такие явные.
Алое многолистный:

Фото: brewbooks on Flickr

Фото: beart.org.uk

Фото: esdrascalderan on Flickr

Фото: mandj98 on Flickr

И тут самое время вспомнить о Золотом Сечении! Ни одни ли из самых прекрасных и гармоничных творений природы изображены на этих фотографиях? И это далеко не все. Присмотревшись, можно найти похожие закономерности во многих формах.
Конечно заявление, что все эти явление построены на последовательности Фибоначчи звучит слишком громко, но тенденция на лицо. Да и к тому же сама последовательность далека от совершенства, как и всё в этом мире.
Есть предположение, что последовательность Фибоначчи - это попытка природы адаптироваться к более фундаментальной и совершенной золотосечённой логарифмической последовательности, которая практически такая же, только начинается из ниоткуда и уходит в никуда. Природе же обязательно нужно какое-то целое начало, от которого можно оттолкнуться, она не может создать что-то из ничего. Отношения первых членов последовательности Фибоначчи далеки от Золотого Сечения. Но чем дальше мы продвигаемся по ней, тем больше эти отклонения сглаживаются. Для определения любой последовательности достаточно знать три её члена, идущие друг за другом. Но только не для золотой последовательности, ей достаточно двух, она является геометрической и арифметической прогрессией одновременно. Можно подумать, будто она основа для всех остальных последовательностей.
Каждый член золотой логарифмической последовательности явлется степенью Золотой Пропорции (z ). Часть ряда выглядит примерно так: ... z -5 ; z -4 ; z -3 ; z -2 ; z -1 ; z 0 ; z 1 ; z 2 ; z 3 ; z 4 ; z 5 ... Если мы округлим значение Золотой пропорции до трёх знаков, то получим z=1,618 , тогда ряд выглядит так: ... 0,090 0,146; 0,236; 0,382; 0,618; 1; 1,618; 2,618; 4,236; 6,854; 11,090 ... Каждый следующий член может быть получен не только умножением предыдущего на 1,618 , но и сложением двух предыдущих. Таким образом экспоненциальный рост в последовательности обеспечивается путем простого сложения двух соседних элементов. Это ряд без начала и конца, и именно на него пытается быть похожей последовательность Фибоначчи. Имея вполне определённое начало, она стремится к идеалу, никогда его не достигая. Такова жизнь.
И всё-таки, в связи со всем увиденным и прочитанным, возникают вполне закономерные вопросы:
От куда взялись эти числа? Кто этот архитектор вселенной, попытавшийся сделать её идеальной? Было ли когда-то всё так, как он хотел? И если да, то почему сбилось? Мутации? Свободный выбор? Что же будет дальше? Спираль скручивается или раскручивается?
Найдя ответ на один вопрос, получишь следующий. Разгадаешь его, получишь два новых. Разберёшься с ними, появится ещё три. Решив и их, обзаведёшься пятью нерешёнными. Потом восьмью, потом тринадцатью, 21, 34, 55...